 | 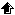 |  | 6.3 Generic modelling approach |
As it is clearly impossible to study the thousands of kilometres of rivers in the largest hydrographic networks, a way around the complexity had to be found. This is why we constructed a mathematical model (RIVERSTRAHLER, [46][]) based on a geomorphological analysis by stream-order []; it takes into account the river network as a regular confluence pattern of tributaries of increasing order with mean characteristics (from orders 1 to 8 in the case of the Seine). The RIVERSTRAHLER model combines a model of the ecological processes (RIVE) and a simplified hydrological model (HYDROSTRAHLER) which takes into account the basin-scale hydromorphological, meteorological and input constraints from point sources (domestic and industrial discharges) and diffuse sources (leaching of rocks and soils). All these constraints are important controlling factors in phytoplankton development.
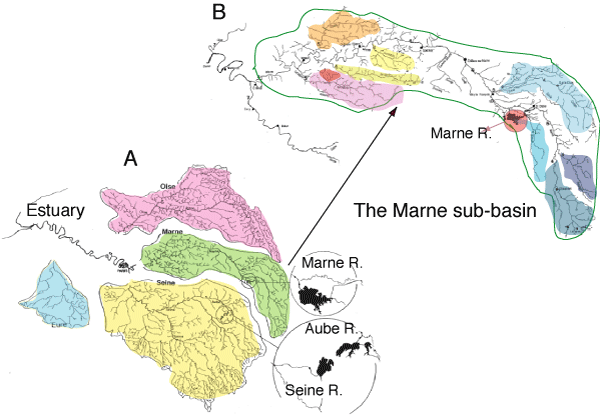
According to the heterogeneity within any watershed on the point of view of the geomorphology, the human activity, etc., the watershed under study can be split into several homogeneous sub-basins, providing that data are available. Here, the Seine was divided into 4 sub-basins (Upstream Seine, Marne, Oise and Eure) whereas two sub-basins were considered for the Scheldt (Upstream Scheldt and Rupel) and the Mosel (Upstream Mosel and Meurthe) and one for the Loire. Note however that for the scenarios of phosphorus reduction explored below, the Marne was divided into 9 sub-basins (Figure 1). The results obtained for each sub-basins are then taken by a model of a main branch, for which the hydromorphology is described every km.
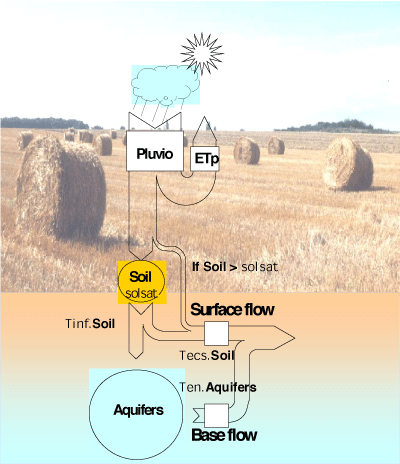
The HYDROSTRAHLER module calculates the hydrology of the whole drainage network, from the morphological characteristics by stream order. Discharge in order n tributaries is calculated as the sum of the discharges of their two n-1 order tributaries, the discharges of lateral tributaries of order 1 to n-1, and the flow from its direct watershed, i.e. the part of the watershed that does not belong to the catchment of the tributaries (see Billen et al. [46]). The latter is calculated from precipitation and potential evapotranspiration data with a classical rain-discharge conceptual model, taking into account the role of a soil and an aquifer reservoir (see e.g. Bultot & Dupriez []). This model, which involves 4 parameters (soil saturation, infiltration rate, internal flow rate, aquifer flow rate), can distinguish between three components of the discharge from the watershed: the base flow supplied by the water table, the internal (or hypodermic) flow supplied by the soil reservoir, and the surface runoff supplied in periods of soil saturation (Figure 2). For some applications of the model, a module describing snow melting can be added ([]; described also in []).
From the value of the discharge (Q, m3 s-1) calculated by stream order, width (w, m), slope (s, m m-1), mean depth (d, m) and flow velocity (v, m s-1) are calculated by rearranging of the Manning's empirical formula [46]. The flow from the direct catchment area of the river, or from its lateral tributaries of lower stream orders, `dilutes' the water masses flowing through the main channel. The corresponding dilution factor and its variations with the stream order and the season are very important for controlling the ecological functioning of rivers.
In the main branch of the river, the calculation is similar, taking into account the contribution to the flow of both the direct watershed and the considered sub-basins. In regulated sectors, the values of the depth and the wetted section are taken into account.
Besides data of rainfall, potential evapotranspiration and air temperature, which are required for the HYDROSTRAHLER model, additional constraints act on the ecological model (Figure 3). Besides inputs (points and diffuse, see above), meteorological constraints such as water temperature, photoperiod and light intensity seasonal variations are represented by sine functions (During the photoperiod, the hourly irradiance is also calculated as a sine function [46].
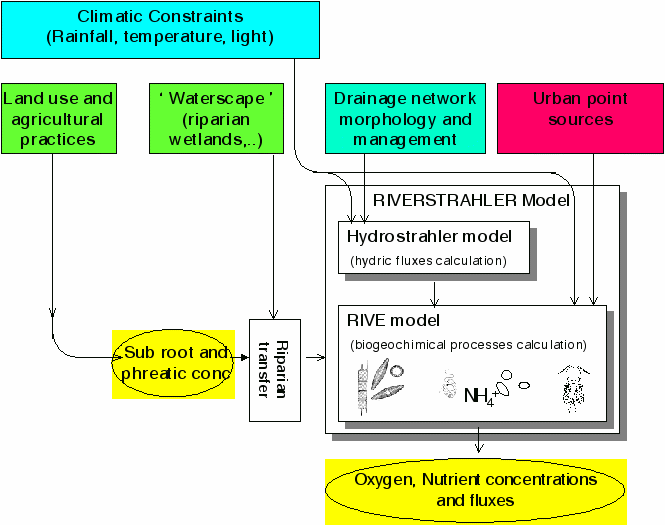
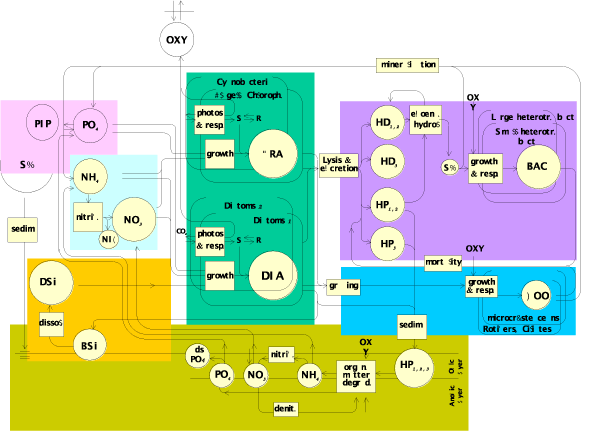
The model of ecological functioning (RIVE model, [46][]) constitutes the common module for the calculation of water quality in the sub-basins and the main branch of the studied river. It consists of 22 variables, including nutrients (nitrate and ammonium, phosphate, dissolved silica), dissolved and particulate organic matter (as two classes of biodegradability), two taxonomic groups of phytoplankton (diatoms and non-diatoms), two groups of zooplankton (rotifers and micro-crustaceans) and bacteria (Figure 4). The description of the phytoplankton dynamics is based on the Aquaphy module by Lancelot et al. [] which distinguishes between photosynthesis -controlled by light intensity- and algal growth -controlled by nutrient availability-. The module has been adapted to two groups of algae (diatoms and non diatoms) and a formulation for loss processes by excretion and grazing has been added [][]. The impact of invasive molluscs such as Dreissena as well as that by viruses is represented by constant rates, modulated by temperature. The degradation of organic matter and bacterioplankton dynamics are described according to the HSB module [][][]. The RIVE model also includes a calculation of nutrient exchanges across the sediment-water interface (Venice) as a result of a given sedimentation flux of organic material, taking into account organic matter degradation, associated ammonium and phosphate release and oxygen consumption, nitrification and denitrification, phosphate and ammonium adsorption onto inorganic material, mixing processes in the interstitial and solid phases and accretion of the sedimentary column by inorganic matter sedimentation [][]. Sedimented biogenic silica is redissolved []. Water column nitrification [] and phosphate adsorption on suspended inorganic particles (and their subsequent sedimentation) are also taken into account in the model.
The kinetics of the major processes involved in the ecological functioning and the corresponding parameters are mostly derived from experimental field work. Essentially, the same kinetic formulations are used in the model applied to any of the rivers. Only the parameter values are occasionally modified within the narrow range of experimental determinations (Table 1). Contrarily to the HYDROSTRAHLER hydrological modelling, the ecological modelling approach is deterministic as the kinetics formulations and parameter determinations are independent from the validation of the model, based on field observations.
A basic assumption behind the RIVERSTRAHLER model is that of the unicity of control processes in the functioning of aquatic ecosystems throughout the entire aquatic continuum. We found that the kinetics of the microscopic processes are identical from upstream to downstream and that the way in which these processes are expressed in situ is entirely conditioned by the constraints (meteorological, hydrological, point and diffuse sources of nutrients, cf. Figure 3) . In literature, whereas most of the nutrient flux modelling approaches are based on a statistical approach at basin scale [][][440][], models of phytoplankton development usually only describe one river sector (on the Rhine: Admiraal et al., []; on the Loire: the POLUPA model by the Agence de lĠEau Loire-Bretagne; on the Lot: Capblancq & Dauta, []; Qotbi, []; on the Mosel: Schöl et al., []; on the Rhine: Schöl et al., []). The RIVERSTRAHLER approach describes the ecological and microbial transformation of nutrients with a multiscaling spatial approach of the hydrographic network and main branch. It differs from the POTAMON model designed for simulating potamoplankton from source to mouth of the main river [].
 |  |  | 6.3 Generic modelling approach |